Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that the phase-space distribution function is constant along the trajectories of the system–that is that the density of system points in the vicinity of a given system point travelling through phase-space is constant with time.
There are also related mathematical results in symplectic topology and ergodic theory.
Contents |
Liouville equation
The Liouville equation describes the time evolution of the phase space distribution function. Although the equation is usually referred to as the "Liouville equation", this equation was in fact first published by Gibbs in 1902.[1] It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838.[2] Consider a dynamical system with canonical coordinates 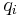 and conjugate momenta
and conjugate momenta 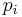 , where
, where 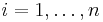 . Then the phase space distribution
. Then the phase space distribution 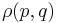 determines the probability
determines the probability 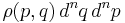 that the system will be found in the infinitesimal phase space volume
that the system will be found in the infinitesimal phase space volume 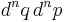 . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of 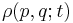 in time
in time  :
:
Time derivatives are denoted by dots, and are evaluated according to Hamilton's equations for the system. This equation demonstrates the conservation of density in phase space (which was Gibbs's name for the theorem). Liouville's theorem states that
- The distribution function is constant along any trajectory in phase space.
A simple proof of the theorem is to observe that the evolution of  is defined by the continuity equation:
is defined by the continuity equation:
That is, the tuplet 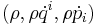 is a conserved current. Notice that the difference between this and Liouville's equation are the terms
is a conserved current. Notice that the difference between this and Liouville's equation are the terms
where  is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density
is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density 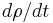 is zero follows from the equation of continuity by noting that the 'velocity field'
is zero follows from the equation of continuity by noting that the 'velocity field' 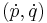 in phase space has zero divergence (which follows from Hamilton's relations).
in phase space has zero divergence (which follows from Hamilton's relations).
Another illustration is to consider the trajectory of a cloud of points through phase space. It is straightforward to show that as the cloud stretches in one coordinate – 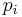 say – it shrinks in the corresponding
say – it shrinks in the corresponding 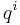 direction so that the product
direction so that the product 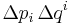 remains constant.
remains constant.
Equivalently, the existence of a conserved current implies, via Noether's theorem, the existence of a symmetry. The symmetry is invariance under time translations, and the generator (or Noether charge) of the symmetry is the Hamiltonian.
Physical interpretation
The expected total number of particles is the integral over phase space of the distribution:
A normalizing factor is conventionally included in the phase space measure but has here been omitted. In the simple case of a nonrelativistic particle moving in Euclidean space under a force field 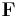 with coordinates
with coordinates 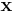 and momenta
and momenta 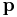 , Liouville's theorem can be written
, Liouville's theorem can be written
This is similar to the Vlasov equation, or the collisionless Boltzmann equation, in astrophysics. The latter, which has a 6-D phase space, is used to describe the evolution of a large number of collisionless particles moving under the influence of gravity and/or electromagnetic field.
In classical statistical mechanics, the number of particles  is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting
is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting 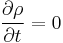 gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by
gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by  equal to any function of the Hamiltonian
equal to any function of the Hamiltonian  : in particular, it is satisfied by the Maxwell-Boltzmann distribution
: in particular, it is satisfied by the Maxwell-Boltzmann distribution 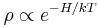 , where
, where  is the temperature and
is the temperature and  the Boltzmann constant.
the Boltzmann constant.
See also canonical ensemble and microcanonical ensemble.
Other formulations
Poisson bracket
The theorem is often restated in terms of the Poisson bracket as
or in terms of the Liouville operator or Liouvillian,
as
Ergodic theory
In ergodic theory and dynamical systems, motivated by the physical considerations given so far, there is a corresponding result also referred to as Liouville's theorem. In Hamiltonian mechanics, the phase space is a smooth manifold that comes naturally equipped with a smooth measure (locally, this measure is the 6n-dimensional Lebesgue measure). The theorem says this smooth measure is invariant under the Hamiltonian flow. More generally, one can describe the necessary and sufficient condition under which a smooth measure is invariant under a flow. The Hamiltonian case then becomes a corollary.
Symplectic geometry
In terms of symplectic geometry, the phase space is represented as a symplectic manifold. The theorem then states that the natural volume form on a symplectic manifold is invariant under the Hamiltonian flows. The symplectic structure is represented as a 2-form, given as a sum of wedge products of dpi with dqi. The volume form is the top exterior power of the symplectic 2-form, and is just another representation of the measure on the phase space described above. One formulation of the theorem states that the Lie derivative of this volume form is zero along every Hamiltonian vector field.
In fact, the symplectic structure itself is preserved, not only its top exterior power. For this reason, in this context, the symplectic structure is also called Poincaré invariant. Hence the theorem about Poincaré invariant is a generalization of the Liouville's theorem.
Further generalization is also possible. In the frame of invariant Hamiltonian formalism, the theorem about existence of symplectic structure on invariant phase space turns out to be a deep generalization of the theorem about Poincaré invariant.
Quantum Liouville equation
The analog of Liouville equation in quantum mechanics describes the time evolution of a mixed state. Canonical quantization yields a quantum-mechanical version of this theorem, the Von Neumann equation. This procedure, often used to devise quantum analogues of classical systems, involves describing a classical system using Hamiltonian mechanics. Classical variables are then re-interpreted as quantum operators, while Poisson brackets are replaced by commutators. In this case, the resulting equation is[3][4]
where ρ is the density matrix.
When applied to the expectation value of an observable, the corresponding equation is given by Ehrenfest's theorem, and takes the form
where  is an observable. Note the sign difference, which follows from the assumption that the operator is stationary and the state is time-dependent.
is an observable. Note the sign difference, which follows from the assumption that the operator is stationary and the state is time-dependent.
Remarks
- The Liouville equation is valid for both equilibrium and nonequilibrium systems. It is a fundamental equation of nonequilibrium statistical mechanics. Its application to dilute gases is called the Boltzmann equation.
- The Liouville equation is integral to the proof of the fluctuation theorem from which the second law of thermodynamics can be derived. It is also the key component of the derivation of Green-Kubo relations for linear transport coefficients such as shear viscosity, thermal conductivity or electrical conductivity.
- Virtually any textbook on Hamiltonian mechanics, advanced statistical mechanics, or symplectic geometry will derive[5] the Liouville theorem.
See also
References
- Modern Physics, by R. Murugeshan, S. Chand publications
- Liouville's theorem in curved space-time : Gravitation § 22.6, by Misner,Thorne and Wheeler, Freeman
- ^ ['Elementary Principles in Statistical mechanics, by J. Willard Gibbs, p9].
- ^ [J. Liouville, Journ. de Math., 3, 349(1838)].
- ^ The theory of open quantum systems, by Breuer and Petruccione, p110.
- ^ Statistical mechanics, by Schwabl, p16.
- ^ [for a paricularly clear derivation see "The Principles of Statistical Mechanics" by R.C. Tolman , Dover(1979), p48-51].
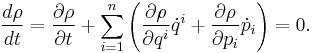
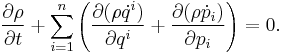
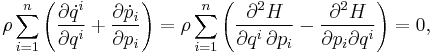
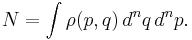
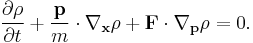
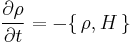
![i\hat{\mathbf{L}}=\sum_{i=1}^{n}\left[\frac{\partial H}{\partial p_{i}}\frac{\partial}{\partial q^{i}}-\frac{\partial H}{\partial q^{i}}\frac{\partial }{\partial p_{i}}\right]=\{\cdot,H\}](/2012-wikipedia_en_all_nopic_01_2012/I/6581f328e1cac0783445912e32239894.png)
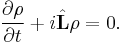
![\frac{\partial \rho}{\partial t}=\frac{1}{i \hbar}[H,\rho]](/2012-wikipedia_en_all_nopic_01_2012/I/16b4e0a7bb9a8a7f5129d608759f975c.png)
![\frac{d}{dt}\langle A\rangle = \frac{1}{i \hbar}\langle [A,H] \rangle](/2012-wikipedia_en_all_nopic_01_2012/I/94a7597fdee8c1e84ce13b82f00a532a.png)